Each of the seven tones of a major or minor scale is represented by a numeral that stands for the triad built using that note. Some chords will naturally come out major, some minor, and we use uppercase numerals for the major ones, lowercase for minor or diminished.
Therefore in a major key - any major key! - the seven triads natural to the key are
I, ii, iii, IV, V, vi, vii°
That little "°" after the vii means it's diminished. Sometimes it is written out as "dim."

Minor scales have several forms, but the most common chords in minor would include a V chord made to be major:
i, ii°, III, iv, V, VI, VII.
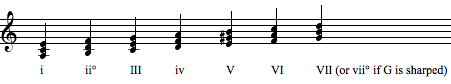
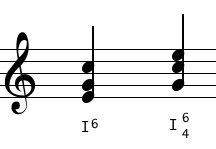
The numerals will often come with numbers attached, and the numbers are survivors of the practice of figured bass that will be discussed in the next section. Let's keep it simple and just list the most common.
If there are no numbers, the chord is in root position, with its root as the bass.
"6" means the chord is in first inversion. That is, the middle note of the original triad is in the bass position, which means somewhere above there will be found the interval of a sixth formed with the bass (or a sixth plus one or more octaves). "6" is short for "6/3" because the other note of the chord will be a 3rd above the bass. But for our purposes just think "6" = "first inversion."
"6/4" (or 6 with a 4 underneath it) means the triad is in 2nd inversion. The original top note is now the bass.
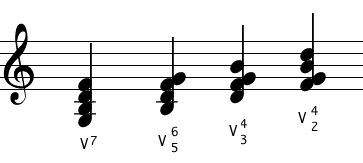
You'll also need the most common ones for seventh chords:
"7" means a root position seventh chord.
"6/5" is a first inversion seventh chord.
"4/3" is a second inversion seventh chord.
"4/2" is a third inversion seventh chord (the seventh itself is in the bass).
If one of these numbers has a flat or sharp by it that means the pitch corresponding to that number is to be raised or lowered from what it would normally be in the key signature.
The next thing you need to know about realizing Roman numeral harmony is that you are not limited to just the tones specified by the numerals. While following the rules of good counterpoint you can add "in between" notes to fill in between chords, and you can introduce dissonances that resolve to a note of the requested chord. Your guide in this as in much of life is J.S. Bach, whose harmonizations are widely available for study. You'll find 30 or more of them in the online Music Library at Ars Nova, and you can open them from within Counterpointer or Practica Musica or Songworks, listen to them, and study their part-writing before you attempt doing some yourself.
How to proceed
A good practice is to begin by sketching in the notes of each harmony needed without regard for counterpoint, then start adjusting for good counterpoint, filling in, etc. It will be easiest if you don't do an entire voice at once, but go beat-by-beat in all voices together. It's OK to change the initial notes that have been provided as a guide. Make use of the suggestions in the next section concerning the addition of passing and neighboring tones and suspensions.
You can frequently press the Evaluate button in Counterpointer to get the program's opinion of how you're doing. It will mark places where the counterpoint needs work or where you have not provided the harmony requested. You'll be following the "Bach vocal" style rules, which are similar to those of 5th species but with movement in all voices and a few additional freedoms.
 Previous
Next
Previous
Next 
Table of Contents
©2009 Ars Nova Software, LLC