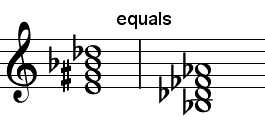Answer: Not everything under the sun has a name, but technically I suppose that on some planets that could perhaps be called an E dim 5 maj 3 min 7.
However, no one ever, to my knowledge, has used that label, mainly because it's enharmonically identical with something much better known. That is, play the same notes on the piano but give them different names, and you have a more reasonable item. Let the G# be read as Ab and the E as Fb and you have a perfectly standard Bb half-dim 7 (Bb m7b5), that is, Bb-Db-Fb-Ab. If the E (that is, Fb) is in the bass then it's in second inversion.
How can you tell it's misspelled? One clue is that a triad generally would not include anything that sounds like a major second, as does that G# to Bb. In a chord, the interval of a second is usually either an inverted seventh or else part of a sus 4 like C-F-G. But this one isn't a candidate for being a sus 4 because the lower tone of the "second" has nowhere to go. When you see a funny-looking interval that's a hint that it's time to try renaming and rearranging some of these notes and see if a more normal identity is available. If you assume that G#-Bb really is Ab-Bb, an inverted seventh, then it's logical to try using its upper note as the root, as I have below.
Often there are also hints to be derived from the function of the chord - where's it going? - but diminished chords are pretty flexible in that way.